0%

Tree(Inorder and Postorder) LEETCODE-100-DAY9

Posted on Edited on Valine:

Inorder

应用场景：

  • BST适用于升序的序列

230.Kth Smallest Element in a BST（BST & Inorder

Given a binary search tree, write a function kthSmallest to find the kth smallest element in it.

Example 1:

1
2
3
4
5
6
7
Input: root = [3,1,4,null,2], k = 1
   3
  / \
 1   4
  \
   2
Output: 1

Example 2:

1
2
3
4
5
6
7
8
9
Input: root = [5,3,6,2,4,null,null,1], k = 3
       5
      / \
     3   6
    / \
   2   4
  /
 1
Output: 3

Follow up:
What if the BST is modified (insert/delete operations) often and you need to find the kth smallest frequently? How would you optimize the kthSmallest routine?

Constraints:

  • The number of elements of the BST is between 1 to 10^4.
  • You may assume k is always valid, 1 ≤ k ≤ BST's total elements.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int count;
    int res;
    public int kthSmallest(TreeNode root, int k) {
        count = k;
        res = 0;
        helper(root);
        return res;
    }
    public void helper(TreeNode root){
        if (root == null) return;
        helper(root.left);
        count--;
        if (count == 0) {
            res = root.val;
        }
        helper(root.right);
    }
}

Postorder

应用场景：

  • 子模块
  • 子树
  • 从底向上

124.Binary Tree Maximum Path Sum

Given a non-empty binary tree, find the maximum path sum.

For this problem, a path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The path must contain at least one node and does not need to go through the root.

Example 1:

1
2
3
4
5
6
7
Input: [1,2,3]

       1
      / \
     2   3

Output: 6

Example 2:

1
2
3
4
5
6
7
8
9
Input: [-10,9,20,null,null,15,7]

   -10
   / \
  9  20
    /  \
   15   7

Output: 42
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
//找左边最大路径或者右边最大路径和拐点(根节点)的值
class Solution {
    int res;//全局变量有值传递和引用传递的区别
    public int maxPathSum(TreeNode root) {
        if (root == null) return 0;
        res = Integer.MIN_VALUE;//求最大值就是 和最小值进行比较
        helper(root);
        return res;
    }
    public int helper(TreeNode root) {
        if (root == null) return 0;
        int left = Math.max(0, helper(root.left));//在这里只取正数
        int right = Math.max(0, helper(root.right));
        res = Math.max(res, left + right + root.val);
        return Math.max(left ,right) + root.val;
    }
}

104.Maximum Depth of Binary Tree

Given a binary tree, find its maximum depth.

The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Note: A leaf is a node with no children.

Example:

Given binary tree [3,9,20,null,null,15,7],

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

return its depth = 3.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) return 0;
        int left = maxDepth(root.left) + 1;
         return Math.max(left, right);
    }
}

第九天LeetCode题目（树的Inorder和Postorder）▼;)

235. Lowest Common Ancestor of a Binary Search Tree（BST）

Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Given binary search tree: root = [6,2,8,0,4,7,9,null,null,3,5]

img

Example 1:

1
2
3
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

Example 2:

1
2
3
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.

Note:

  • All of the nodes’ values will be unique.
  • p and q are different and both values will exist in the BST.
1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root.val > p.val && root.val > q.val) {
            return lowestCommonAncestor(root.left, p, q);
        } else if (root.val < p.val && root.val < q.val) {
            return lowestCommonAncestor(root.right, p, q);
        } else {
            return root;
        }
    }
}

270. Closest Binary Search Tree Value(BST)付费题

找出BST中离Target值最接近的节点

1
2
3
4
5
6
7
8
9
10
11
12
public int ClosestValue(TreeNode root, double target) {
  int res = root.val;
  while (root != null) {
    //每次和res比较，看哪个更小，看比target大还是小，就知道走左还是右
    if (Math.abs(target - root.val) < Math.abs(tartget - res)) {
    	res = root.val;
  	}
  		root = root.val > target ? root.left : root.right;
  	}
  		return res; 
	}
}

173. Binary Search Tree Iterator（BST & Inorder）

Implement an iterator over a binary search tree (BST). Your iterator will be initialized with the root node of a BST.

Calling next() will return the next smallest number in the BST.

Example:

img

1
2
3
4
5
6
7
8
9
10
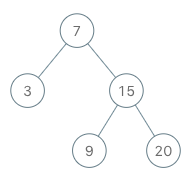
BSTIterator iterator = new BSTIterator(root);
iterator.next();    // return 3
iterator.next();    // return 7
iterator.hasNext(); // return true
iterator.next();    // return 9
iterator.hasNext(); // return true
iterator.next();    // return 15
iterator.hasNext(); // return true
iterator.next();    // return 20
iterator.hasNext(); // return false

Note:

  • next() and hasNext() should run in average O(1) time and uses O(h) memory, where h is the height of the tree.

  • You may assume that next() call will always be valid, that is, there will be at least a next smallest number in the BST when next() is called.

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    //中序遍历从小到大递增
    class BSTIterator {
        private TreeNode cur;
        private Stack<TreeNode> stack;

        public BSTIterator(TreeNode root) {
            cur = root;
            stack = new Stack<>();
        }
        
        /** @return whether we have a next smallest number */
        public boolean hasNext() {
            if (!stack.isEmpty() || cur != null) {
                return true;
            }
            return false;
        }

        /** @return the next smallest number */
        public int next() {
                while (cur != null) {
                    stack.push(cur);
                    cur = cur.left;
                }
                cur = stack.pop();
                int val = cur.val;
                cur = cur.right;
                return val;
        }
    }

285. Inorder Successor in BST(BST & Inorder)

在BST中找给定节点P的下一个节点是什么

1
2
3
4
5
6
7
8
9
10
11
12
13
public TreeNode InorderSuccessor(TreeNode root, TreeNode p) {
  //判断当前节点和节点P谁的值大
  TreeNode res = null;
  while (root != null) {
    if (root.val <= p.val) {
      root = root.right;
    } else {
      res = root;//root节点可能就是res
    	root = root.left;
      
  }
  return res;
}

99. Recover Binary Search Tree（BST & Inorder）

Share

Two elements of a binary search tree (BST) are swapped by mistake.

Recover the tree without changing its structure.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Input: [1,3,null,null,2]

   1
  /
 3
  \
   2

Output: [3,1,null,null,2]

   3
  /
 1
  \
   2

Example 2:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Input: [3,1,4,null,null,2]

  3
 / \
1   4
   /
  2

Output: [2,1,4,null,null,3]

  2
 / \
1   4
   /
  3

Follow up:

  • A solution using O(n) space is pretty straight forward.
  • Could you devise a constant space solution?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    TreeNode first = null;
    TreeNode second = null;
    TreeNode prev = null;//记录前一个节点,总比前一个节点大(二叉树性质)
    public void recoverTree(TreeNode root) {
        if (root == null) return;
        helper(root);
        int temp = first.val;
        first.val = second.val;
        second.val = temp;
    }
    public void helper(TreeNode root) {
        if (root == null) return;
        helper(root.left);//从左边的叶节点开始执行， 
        if (prev != null && prev.val >= root.val) {
            if (first == null) first = prev;
            second = root;
        }
        prev = root;
        helper(root.right);
    }
}

124. Binary Tree Maximum Path Sum（Postorder）

Given a non-empty binary tree, find the maximum path sum.

For this problem, a path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The path must contain at least one node and does not need to go through the root.

Example 1:

1
2
3
4
5
6
7
Input: [1,2,3]

       1
      / \
     2   3

Output: 6

Example 2:

1
2
3
4
5
6
7
8
9
Input: [-10,9,20,null,null,15,7]

   -10
   / \
  9  20
    /  \
   15   7

Output: 42
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//找左边最大路径或者右边最大路径和拐点(根节点)的值
class Solution {
    int res;//全局变量有值传递和引用传递的区别
    public int maxPathSum(TreeNode root) {
        if (root == null) return 0;
        res = Integer.MIN_VALUE;//求最大值就是 和最小值进行比较
        helper(root);
        return res;
    }
    public int helper(TreeNode root) {
        if (root == null) return 0;
        int left = Math.max(0, helper(root.left));//在这里只取正数
        int right = Math.max(0, helper(root.right));
        res = Math.max(res, left + right + root.val);
        return Math.max(left ,right) + root.val;
    }
}

250. Count Univalue Subtrees(Postorder)付费题

有多少个Subtree有同样的val

HINT:dango:：单独的叶子节点也算一个子树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//PostOrder
//time:O(n)遍历一遍
//space:O(n)
int res;
public int countUnivalueSubtrees(TreeNode root) {
  res = 0;
  helper(res);
  return res;
}
public boolean helper(TreeNode root) {
  if (root == null) return true;
  boolean left = helper(root.left);//子树为空的时候为TRUE
  boolean right = helper(root.right);
  
  if (left && right) {
    if (root.left != null && root.val != root.left.val) {
      return false;
    }
    if (root.right != null && root.val != root.right.val) {
      return false;
    }
    res++;
    return true;
  }
  return false;
}

236.Lowest Common Ancestor of a Binary Tree（Postorder)

Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Given the following binary tree: root = [3,5,1,6,2,0,8,null,null,7,4]

img

Example 1:

1
2
3
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.

Example 2:

1
2
3
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.

Note:

  • All of the nodes’ values will be unique.
  • p and q are different and both values will exist in the binary tree.
1
2
3
4
5
6
7
8
9
10
11
12
13
//Preorder是从上到下，Postorder是从下到上
//typical, needs to be memorized
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null || root == p || root == q) return root;
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        if (left != null && right != null) {
            return root;
        }
        return left == null ? right : left;//叶子节点，或者单子树节点
    }
}

366. Find Leaves of Binary Tree（Postorder)付费题

找出BST中所有的叶子节点

[4, 5, 3] [2] [1]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public List<List<Integer>> findLeaves (TreeNode root) {
  //有顺序，就要有一个level
  List<List<Integer>> res = new ArrayList<>();
  helper(res, root);
  return res;
}
private int helper(List<List<Integer>> res, TreeNode root) {
  if (root == null) return -1;
  int left = helper(res, root.left);
  int right = helper(res, root.right);
  int level = Math.max(left, right) + 1;//叶子节点是第0层，因为叶子节点也有左右子树，都为0，为NULL层
  if (res.size() == level) {
    res.add(new ArrayList<>());
  }
  res.get(level).add(root.val);//将值加入对应层
  root.left = null;
  root.right = null;
  return level;
}